More and more scientists are studying complex systems. Is a new field of study arising, or is science simply getting more complicated?

There is a funny dance that some Chicago physicists and biologists do when the topic of complexity theory comes up. They squirm, skirt the issue, dodge the question, bow out altogether unless they’re allowed alternative terms. They twirl the conversation toward their own specific research projects: yes, the projects involve systems that are “rich” and “complicated” and not explained by natural laws of physics; yes, systems that develop universal structures which appear in other, completely different systems on a range of scales; yes, systems that begin with simple ingredients and develop outcomes that are—there’s no other word for it—complex.

View the movies E. Coli colony formation Raleigh-Taylor Instability Raleigh-Taylor close-up Flame convection

“The problem with complexity is that it has become a buzzword,” says Heinrich Jaeger, professor in physics and the James Franck Institute. “What do we mean when we say complex? That something is more complicated than its simple components imply? Why not say complicated?” he asks. “Complexity is a newer word, has a better ring. The word itself has taken on an aura; it’s become a label for a lot of things to a lot of people.” And that, he says, is a good reason to avoid it: buzzwords are hard to pin down and therefore inherently dangerous.

Jaeger’s wariness is well founded. A lazy woman’s Lexis-Nexis search for complexity theory attests to the term’s recent popularity. The search brings up lots of business articles on topics ranging from Southwest Airlines’ air-cargo system (modeled on the complex swarming tendencies of ants) to fluctuations in stock prices. An equally large number of popular-science stories come up, typically painting an image of a theory to unlock all mysteries. More often than not these articles cite researchers at the interdisciplinary, 18-year-old Santa Fe Institute, whose single-minded insistence that laws of complexity can explain nearly any phenomenon rankles many an academic.

Yet academics aren’t immune to the fever. In April 1999 Science magazine ran a special issue in which distinguished researchers reflected on how “complexity” has influenced their fields. As evidence of academe’s move into the realm of the complex, one article cited an academic building boom in multidisciplinary science centers—including Chicago’s nascent Interdisciplinary Research Building. This fall’s release of computer-science wunderkind Steven Wolfram’s tome A New Kind of Science resulted in a flurry of articles about whether simple, fundamental laws, as Wolfram argues, can explain all things complex—including evolution and free will. (Physics Nobel laureate Steven Weinberg argued in the New York Review of Books that they most emphatically cannot.

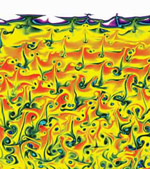
Researchers at the Flash Center simulate the highly complex interactions within exploding stars. As shown here, helium on the surface of a neutron star can burn so vigorously that a detonation wave—a shock wave followed closely by a burning region—forms, moving across the star’s surface at 1⁄30 the speed of light. After 150 microseconds the helium converts to nickel.

Judging from the press, complexity theory is on the verge of, if not already, changing the world.

The buzz is enough to drive many researchers away from the term. But one Chicago physicist is more than willing to use the term complexity. Two years ago he gave the University’s annual Nora and Edward Ryerson Lecture on the topic, titled “Making a Splash, Breaking a Neck: The Development of Complexity in Physical Systems,” and he contributed “Some Lessons from Complexity” to Science’s special complexity issue. He will name names when asked who else at Chicago might provide insight into the rise in studies of complex systems. (“I know Leo said this is what I study, but...” is a common conversation starter.)

The “Leo” in question is bright-eyed, white-bearded Leo P. Kadanoff, the John D. MacArthur distinguished service professor in physics and mathematics, the James Franck and Enrico Fermi Institutes, and the College. A National Medal of Science winner and a founder of the soft condensed-matter field in physics, Kadanoff has mused over complexity theory for the past three decades. What he will tell you is that, despite what the press says, there is no theory—no set of laws—of complexity. Only lessons and “homilies.”

A definition of the nature of complexity, Kadanoff says, “has been somewhat elusive.” But if one were to try, “what we see is a world in which there seems to be organization built up in some rich and interesting fashion—from huge mountain ranges, to the delicate ridge on the surface of a sand dune, to the salt spray coming off a wave, to the interdependencies of financial markets, to the true ecologies formed by living things. For each kind of organization, we want to understand how it arose and whether it has any general rules associated with it.”

The “metachallenge” in seeking these rules, he says, is, “What can you learn from one complex system that you can apply to another? Even though there are not any laws of complexity, there are experiences that you can have with one complex system that will help you study another. Even in systems which are very complex, there are aspects of their behavior which might be simple and predictable.”

The job as Kadanoff and others at the University see it, regardless of their willingness to label the systems they study complex, is “to reach into these systems to try to distinguish between the things that are predictable and not predictable; in the ones that are predictable to try to pick out the universal features, and then to do something to characterize the unpredictable parts.” 

That’s the driving force behind complexity studies: to characterize what has for so long eluded characterization. “Complexity,” reflects physics professor Tom Witten, “is where a system is more ordered than random because it can be described in a nutshell. The nutshell might be big, but you can describe what’s going on. And the more you discover, the more payoff you get, because you have simplified [what’s being described] below what it was at the outset. The good thing is that you’ll never reach the task’s end, and you’re often rewarded by finding more.

“I never think about whether something is complex,” Witten reiterates. “I think about things because they are intriguing—and wouldn’t it be terrible if I ever got a complete nutshell?”

Stroboscopic pictures of a drop of water falling from a pipette. The shape of the drop's neck is universal, that is, independent of the experimental setup. Yet there's unpredictability too: who knows how far the neck will stretch before it snaps?

What counts as a complex—complicated, rich, interestingly organized, needing-a-big-nutshell—system depends on the eye of the beholder.

Chicago researchers study what might seem mundane: how grains arrange themselves, for example, or how a drop of liquid breaks apart, or how a surface crumples. And they study what seems almost overwhelmingly complicated: for example, how an entire star manages to explode, or how the genomic architecture of E. coli is naturally programmed to lead the single-celled bacterium to form colonies and communicate as a multicellular, highly evolved organism.

The last is the work of biochemistry & molecular biology professor James Shapiro. Complexity watchers might have seen Shapiro last year in the New York Times and the Economist during a minor media flurry over the founding of the Institute for Complex Adaptive Matter (ICAM), an independent unit of the Los Alamos National Laboratory and the University of California, Berkeley. He presented a highly quotable lecture on migration patterns created by colonies of the bacteria Proteus mirabilis. The Economist lauded his research for “illuminating problems as diverse as disease, water treatment, corrosion, and the formation of certain metal ores.

The Flash Center’s simulations can reach an unprecedented level of detail, as demonstrated by these Gordon Bell Prize–winning results from a full, multiphysics calculation of a nuclear detonation within an exploding star.

Biological systems, even physicists agree, are as complex as a system comes. Although Shapiro, like most of his colleagues, is wary of the term complexity theory, he believes the ideas that arise from studying complexity are opening new realms of study for biologists.

“For the physicist, the properties of a complex system emerge out of the individual interactions that compose it,” says Shapiro in his second-floor Cummings Life Science Center office—a block away from the Research Institutes where Jaeger, Kadanoff, Witten, and colleagues muse over complex physical systems. “They look at complexity as systems with many interacting components and then somehow these systems develop interesting properties.” He’s right. When Kadanoff refers to the complexity apparent in the delicate ridge of a sand dune or the salt spray coming off a wave, he is conjuring the complicated outcomes that can arise when simple grains of sand or water molecules are placed under certain conditions: high winds, for instance.

A growing number of biologists, Shapiro argues, approach complexity from an entirely different angle. “Biological systems are very complicated and very complex, but they have clear functionalities. For organisms things have to be done and done right.” What interests biologists, he says, is how the organism uses complexity to adapt. “While the physicist asks, How does complexity generate something that is describable with pattern to it, the biologist asks, How does the organism use complexity to achieve its objectives?”

And where physicists are interested in characterizing the unpredictable outcomes of a complex system—the magnitude and direction of a sand-dune avalanche, or the trajectories and sizes of sea-spray droplets—there is a notable absence of chaos in the systems biologists study. That fact alone is intriguing. “Why is it that biological systems are so unbelievably complex but work so reliably?” asks Shapiro. “Why don’t they undergo chaotic transitions? What allows biological systems to utilize complexity but not to be overwhelmed by it?”

Finding the answers, he believes, depends upon understanding two things: how the large numbers of components in biological systems interact to create precise functional behavior, and how basic principles of regulation and control operate at all levels in living organisms. Applying those concepts to genetics requires a shift toward what Shapiro has called “a 21st-century view of evolution.”

The past 50 years of genetic research, he argues, have provided clear evidence to contradict the prevailing theory that organisms evolve in a “random walk” from adaptation to adaptation. Rather, evolution is the result of “natural genetic engineering”—a highly refined and efficient problem-solving and genetic-reorganization process carried out by a genomic architecture that is, he notes, remarkably similar to a computational system. The information processing occurs in an organism’s cells via molecular interactions, and the data on which the processing runs is stored in the DNA.

Swirls are universal elements of turbulence, appearing in exploding stars and, more simply, in fluid flowing past an obstacle. The result shown above is the characteristic von Kármán street pattern.

Contrary to popular belief, “the character of an organism is not determined solely by its genome,” Shapiro maintains. “By itself, DNA is inert.” Instead, survival and reproduction are the result of how cells’ information-processing systems evaluate multiple internal and environmental signals and draw on the data stored in DNA to adapt quickly and reliably. “Cells have to deal with literally millions of biochemical reactions during each cell cycle and also with innumerable unpredictable contingencies,” Shapiro noted at the 2001 International Conference on Biological Physics in Kyoto, Japan. The constantly looming unpredictability doesn’t overwhelm the system because, as Shapiro explains in a 1997 Boston Review article, “all cells from bacteria to man possess a truly astonishing array of repair systems which serve to remove accidental and stochastic sources of mutation. Multiple levels of proofreading mechanisms recognize and remove errors that inevitably occur during DNA replication.”

In fact, cells protect themselves against “precisely the kinds of accidental genetic change that, according to conventional theory, are the sources of evolutionary variability.”

If accidents don’t cause evolution, what does? The primary perpetrators of evolutionary change, Shapiro says, are mobile genetic elements—DNA structures found in all genomes that can shuttle from one position to another in the genome, cutting and splicing like a Monsanto engineer. Thanks to these mobile little guys, he notes in the Review, “genetic change can be specific (these activities can recognize particular sequence motifs) and need not be limited to one genetic locus (the same activity can operate at multiple sites in the genome). In other words, genetic change can be massive and nonrandom.”

Shapiro’s contribution to the new view of evolution is to demonstrate that the elements in the computational genome are universal beyond people, plants, and animals. Bacterial genomes, his work demonstrates, also operate and evolve via natural genetic engineering. The process is not random; it’s in- fluenced by the bacteria’s experience. Moreover, bacteria experience their environment not as individual cells oblivious to others in the colony, but as a multicellular organism. This is evident in the patterns they create.

“That the patterns exist tells us that the bacteria are highly organized, highly differentiated, and highly communicative,” he explains. “In biology when you see regularity and pattern and control working, you say, Well, what is it functionally related to, what’s the adaptive utility for the organism?”

Heinrich Jaeger’s MRSEC group attempts to control complexity—first by understanding how granules “self-assemble” and then guiding that assembly. One result is these gold nanoparticle chains on a diblock copolymer template.		These silver nanowires are the result of allowing the nanoscopic particles to follow their natural “bootstrapping” tendencies to clump in rows. Jaeger’s group merely controls the conditions: the temperature, pressure, and the template’s chemical makeup.

On his Macintosh PowerBook Shapiro points his browser to his Web site, where he’s posted movies of bacteria colonies growing and migrating. Running in black and white, the QuickTime films have the scratchy monochromatics of the silent era. One depicts five E. coli cells scattered on agar. The squirmy, haloed cells begin growing and dividing, and then the daughter cells grow and divide, and soon there are five little colonies surrounded by halos. “The daughter cells are clearly interacting,” says Shapiro. “What I am interested in is, are they interacting because they’re communicating or simply because each cell is internally programmed independently of the other cell? The way to tell is by looking at what happens when the scattered colonies encounter one other.”

The five colonies seem to seek each other out, growing first toward each other, meeting and merging, then spreading outward en masse. “The very least you can say from this observation is that E. coli cells maximize cell-to-cell contact.” How the cells communicate with each other—whether they sense a chemical signal, perhaps in the halo, or a physical signal from the other bacteria—has yet to be determined. “But that they interact,” says Shapiro, “is quite clear.”

Another film depicts an E. coli colony advancing across a petri dish on which a glass fiber lies diagonally. The edge of the colony moves along until, boop!, it hits the fiber’s top end. Suddenly the bugs at the colony’s own top edge are released. They use their flagella to swim around the fiber, nosing into it and wiggling vigorously. “According to conventional wisdom and how they were grown,” says Shapiro, “those individual cells shouldn’t have been motile.” Meanwhile, the lower edge of the colony has not yet met the fiber; its slow advance continues. Shapiro points out that the cells around the fiber swim and divide but do not spread over the agar; only the older, organized colony expands over the surface. After two hours the colony’s lower edge meets the fiber’s lower diagonal. The colony spends some time on the fiber, filling in its mass, before eventually spreading past it and continuing to advance. Yet, rather than being swept up and carried along like picnic crumbs on the backs of ants, the fiber remains in place. “That tells you that the whole colony is not expanding; just the region at the edge is moving outwards,” explains Shapiro. “There’s a small zone of active movement, and then everything stays in place.” The colony expands over the agar not simply by cells dividing and spilling over; rather, an organized structure is at work.

Shapiro’s movies of Proteus mirabilis reveal an even more organized growth and migration structure. In Proteus specialized cells called swarmers are responsible for colony spreading. After a period of eating and dividing, the colony releases swarmers outward; the expanded colony pauses, eats and divides, and eventually sends more swarmers out. The resulting pattern is a series of rings similar to a tree’s. Swarmer cells, Shapiro notes, move only in groups—isolated, they go nowhere—and they do not divide. Short, fat cells are responsible for cell multiplication. In a way that may suggest a supercomputer coordinating the activity of large numbers of interconnected processors, the expanding Proteus colony coordinates the movement of large numbers of swarmer cells.

Without the focus on the issues of complexity, Shapiro believes, biologists would be at a loss to explain the behavior he’s caught on film. “In biological systems, at least, trying to understand how the components of these complicated, complex systems interact and do something adaptive is central to understanding them at a deeper level and probably,” he adds, “to understanding all of nature.”

Back the lens out several hundred thousand light years and expand the frame exponentially. A neutron star, its surface roiling in flame and gas—this time in full, glorious color—explodes.

Talk about complex. Now imagine reenacting it.

That’s what a long row of academic posters in the fourth-floor hallway of the Research Institutes Building on Ellis Avenue is dedicated to: simulations of the complex interactions that contribute to a supernova and other exploding stars. This gallery of fantastic images and nearly incomprehensible astrophysical explanations is the work of the federally sponsored Accelerated Strategic Computing Initiative’s (ASCI) five-year-old Center for Astrophysical Thermonuclear Flashes.

“Part of the challenge—what’s fun—is to take apart a complicated pattern. There’s an art to this. It’s not cut and dried; there’s no recipe for a supernova as yet,” says Robert Rosner, the center’s associate director and the William E. Wrather distinguished service professor in astronomy & astrophysics, physics, the Enrico Fermi Institute, and the College. (Until his October appointment as chief scientist at Argonne National Laboratory, Rosner was the center’s director.) “We have to figure out how to take it apart into simpler pieces. Sometimes we get something that is, as yet, impossible to understand. The trick is to get pieces that we can explain and to reassemble these understood pieces into a whole which we can comprehend as an explanation of how an evolved star explodes.”

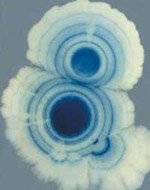
Two E. coli colonies, though grown a day apart, express similar patterns by turning on and off the enzyme beta-galactosidase. Their rings’ alignment tells biologist Shapiro that the periodic enzyme expression is controlled by a chemical field in the growth medium and is not intrinsic to each colony.

Where the computation metaphor allows Shapiro to consider bacteria as highly organized, problem-solving organisms, the nutshells that Rosner’s group wraps around supernovae are equations that, when crunched, create simulations. The orgy of brilliant, curving, flaming gases depicted in “Helium Detonations on Neutron Stars” is one of the largest nutshells the center has obtained to date. The image (on pages 38–39) is the result of an integrated calculation, one that involves many subsidiary calculations conveying all the smaller complicated interactions and chaos-producing dynamics. Together they create a massive burst of exploding helium on the surface of a hypothetical collapsed star that’s dense with closely packed neutrons. Before the group could simulate the burst—much less a supernova—it first had to find the correct equations to describe a detonation, regardless of whether it occurs in a star or a laboratory.

“We ask first, can we understand these events in isolation, separate from their environment and other events? An exploding star, whether a detonation on the surface of a neutron star or an explosion within a white dwarf, leading to a supernova, involves not just detonation, but flames—deflagration—and instability. What happens, for example, when we put a heavy fluid on top of a light fluid?” Rosner asks. “If we can answer those questions, we move up from there.”

A heavy fluid (cold, dense fuel) sinking into a light fluid (hot ashes) during a nuclear burn—the so-called Raleigh-Taylor instability, which the center’s research scientist Alan Calder has modeled—creates turbulence, or chaotic flow in a fluid, which is physicist Kadanoff’s speciality. The center’s simulation of the Raleigh-Taylor instability, an abstract pitching wave of reds, yellows, and oranges (on pages 44–45), confirms what Rosner, Kadanoff, and other physicists already know: that the more minute the detail they try to define in the fluid’s resulting structure of swirling plumes, the more it eludes them. “The deeper you look at this thing, it never settles down,” says Kadanoff.

Turbulence, Rosner explains, is a “real-life exhaustive problem” that presently lies beyond researchers’ predictive abilities. It mystifies them not only in simulations of stellar bodies but also in understanding how coffee and cream move when stirred. “The challenge for experimentalists,” he says, “is to measure at every point the fluid’s temperature, its flow velocity, and density.” Turbulence lies within the realm of complexity that at best, as Kadanoff put it, researchers “do something to characterize.”

The ability to simulate an experiment and remain faithful to what actually happens, Rosner says, to look at “fully turbulent” systems, like those in a neutron star rather than in a coffee cup, and know exactly what is happening, will “bring simulations to another realm of experimental science.”

The turbulence problem underscores a larger point in studies of complex systems. Physical experiments and equation-crunching simulations must for the foreseeable future at least maintain a symbiotic relationship. Given the level of unpredictability in complex systems, using one without the other is like going blind in one eye: you lose depth perception.

In his office Heinrich Jaeger has a poster of a rail yard filled with open boxcars. The cars are piled high with grain, sloping against a cornflower-blue sky. Perched on one boxcar’s top edge is a man reading a newspaper. As the photographer no doubt intended, the man snags the viewer’s eye, and the grain piles recede into the background.

But not for Jaeger. What Jaeger sees are universal elements and unpredictability in those grain piles. How they pile, what triggers an avalanche, how most flowed through the chute that shot them into the boxcars, how some jammed: these are the complex behaviors Jaeger wishes to describe. While Rosner and Kadanoff think in equations and at computer screens, Jaeger and his colleagues in the Materials Research Science and Engineering Center (MRSEC) work with actual matter: grains, fluids, and various surfaces. Theirs are the experiments that feed simulations, and the experiments they conduct aim to reduce a complex system to its simplest, easiest-to-observe components.

“Much of modern scientific work in pattern formation and pattern recognition,” Sidney Nagel, professor in physics and the James Franck Institute, reflects in a 2001 Critical Inquiry essay, “is an attempt to put what the eye naturally sees and comprehends into mathematical form so that it can be made quantitative.” Where most viewers might skim over the monotonous grain piles, Jaeger observes their patterns and behavior, composing equations to describe their dynamics; Nagel’s patterns of choice, meanwhile, are the elongated necks of dripping drops of fluid. “I am seduced by the shape of objects on a small scale,” Nagel’s essay continues. “The forces that govern their forms are the same as those that are responsible for structures at ever increasing sizes; yet on the smaller scale those forms have a simplicity and elegance that is not always apparent elsewhere.”

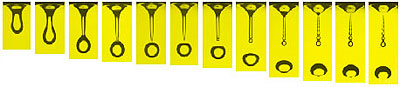
Bacteria’s pattern making reveals their complex nature. Inoculated at different times, these Proteus mirabilis colonies remain independent of each other. Although each expands the same way—swarming and then consolidating—the resulting concentric terraces, explains biologist James Shapiro, do not align because each cycle is controlled by internal population dynamics.

For condensed-matter physicists such as experimentalists Nagel and Jaeger and theorist Witten, even when objects are reduced to their simplest forms, there is always an element of wide-eyed wandering. “Serendipity is OK. A bubbly atmosphere is extremely powerful. The key is that when you find something good, you need to realize it,” says Jaeger. “There is no clear goal. But when you’re awake while wandering around, when you’re paying attention, and something comes along that’s exciting, you can pick it up. It’s a high-risk, high-payoff approach—and the preferred approach if you’re charting territory no one’s been in before.”

It’s the only approach a researcher can take with complex systems. Jaeger’s granular materials, from the nanoscale to the scale of marbles, fall in the realm of complexity (though he prefers complicated) because they often defy what’s already known in condensed-matter physics. Taken together, “large conglomerations of discrete particles,” he and Nagel propose in a 1996 Physics Today article, “behave differently from any of the other standard and familiar forms of matter: solid, liquids, and gases, and [granular material] should therefore be considered an additional state of matter in its own right.” Nagel’s stretched fluid necks, similarly, are nonlinear: too many phenomena are involved to be accounted for in linear equations. Down the hall Witten studies the nonlinear behavior of distorted matter: the crumpling of silver Mylar paper, and on a more minute level, of polymers packed into a small space.

Once the physicists are set free from linear reasoning, they can set about seeking the complex forms’ universals and characterizing their unpredictables. What Nagel has discovered is that all drops breaking apart, regardless of their size, experience a “finite time singularity”—their necks grow infinitely thinner and the forces acting on them infinitely larger until the infinite becomes finite, and the neck breaks. The break-up is a universal element repeated in all drops, of any size and any fluid. Witten, meanwhile, sees analogous singularities in the peaks and ridges of a thin crumpled sheet. These singularities do not develop at a moment in time like Nagel’s. Instead, one approaches the singular shapes by making the sheets thinner and thinner. By examining the limiting behavior of these sheets, he finds universal shapes on scales ranging from cell walls to mountain ranges. The next nutshell to wrap around the phenomenon is why and where different-sized ridges buckle during crumpling; his guess is that the distribution of various sized ridges and peaks is also universal from material to material.

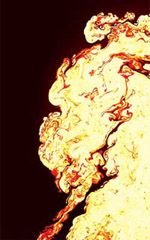
Successfully calculating complexity and displaying the results are two different animals. Although the level of detail achieved in the Flash Center’s full simulation of the Raleigh-Taylor instability above is greater than experiments can capture, even the blown-up image below can’t show all the detail contained in the computational data.

These MRSEC experiments and others like them are the building blocks for simulations created by Rosner’s and Kadanoff’s groups. “Simulators,” Rosner notes, “solve equations. We must ask, first, Are we solving the right equations, and second, Are the equations correctly solved? Experimentalists tell us whether we’re solving the right equations. Can our calculations produce what the experimentalists can measure in the lab? The next question is, Can we solve problems that are produced in nature? Somewhat. But that answer will change in the coming decade.” (He estimates that in three years turbulence simulations will be cracked.)

Just as Rosner is still unable to precisely simulate full turbulence, graduate students in Kadanoff’s group have been unable to fully simulate all the details observed in an experiment by Nagel’s graduate students. Nagel’s team uses strobe photography to capture what happens in the lab: a fluid placed in a strongly charged electric field rises in a mound toward an electrode. The fluid comes to a point, and some motion occurs between fluid and electrode, resolving itself in a form strikingly similar to a lightning bolt. After the bolt flashes, in the space between the fluid and the electrode a spray of fine water droplets—something like rain—appears. Kadanoff’s group has been able to simulate only as far as the mound rising to a point; the outcome, lightning and rain, is still too complex for equations.

“There is a lesson from this,” Kadanoff noted in his 2000 Ryerson lecture. “Complex systems sometimes show qualitative changes in their behavior. Here a bump has turned into lightning and rain. Unexpected behavior is possible, even likely.”

To study complexity, as Kadanoff has remarked, is to attempt to say something about the “interesting” organization of the world around us, to quantify what seems simple yet defies quantification. It is a search for metaphors that, like Shapiro’s use of a computation framework, open new ways of thinking. “When a system transitions from simple to complex is something that I wouldn’t know how to define,” Shapiro reflects. “And I think that’s actually a great problem: how do we distinguish between what we call simple and what we call complex? Even things that seem simple, when you look at them in enough detail, they inevitably become more complex.”

But the idea, Witten observes, “is that there’s a magic way to say what’s happening, where once you say one further thing, the rest is simple. Is that what complexity means, or is that just the purpose of science?”